Mätetal för leverantörsstruktur
I ett tidigare inlägg belystes den klassiska frågan om man ska ha fler eller färre leverantörer, men det inlägget begränsade sig till numerären. Det kanske är ännu mer intressant att diskutera hur leverantörsstrukturen ska se ut. Exempelvis kan man fråga sig om man bara ska ha stora leverantörer eller om det ska vara en mix av stort och smått eller bara små. För att kunna arbeta med leverantörsstrukturen så behövs mätetal. Tyvärr har inte något standardmätetal etablerat sig utan det finns en hel del varianter, exempelvis:
– Antal leverantörer per inköpskategori
– Genomsnittlig spend per leverantör (+ spridningsmått)
– ABC-analys per inköpskategori
– 20/80-analys per inköpskategori
– Exponentialfunktion
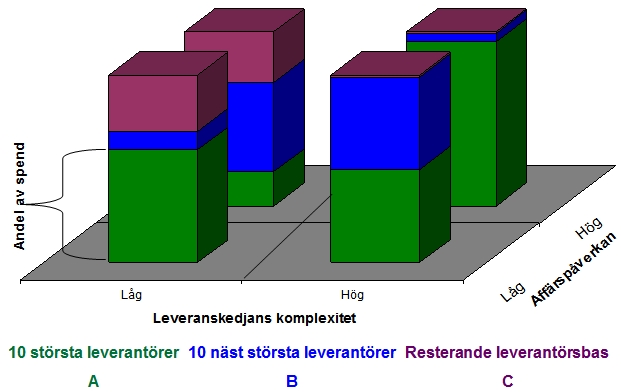
De helt klart dominerande mätetalen verkar vara ABC och 20/80. Dessa metoder är egentligen grova förenklingar av Paretos lag, som är en matematisk modell. Per inköpskategori delas leverantörerna in i grupper beroende på storleken på respektive inköpsvolym. Exempelvis kan det se ut på följande sätt när volymerna kategoriseras enligt Kraljic:
Leverantörsstruktur / Leverantörstäthet
Ur en sådan här bild är den här modellen enkel att förstå, men det krävs tre mätetal per kategori för att beskriva strukturen. Modellen är dessutom ganska grovyxad, dvs enstaka leverantörer som faller över eller under ett gränsvärde kommer att påverka bilden.
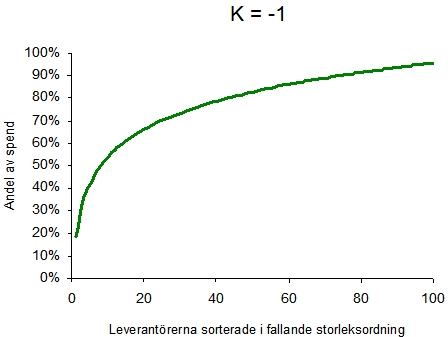
En betydligt mer sofistikerad modell är att anpassa en exponentialfunktion till leverantörs-spend-data. Detta är förvisso också att förenkla Paretos lag, men ger betydligt högre precision än att bara dela upp i delmängder. En ganska klassisk anpassning kan se ut på följande sätt:
Exponentialfunktion k = -1
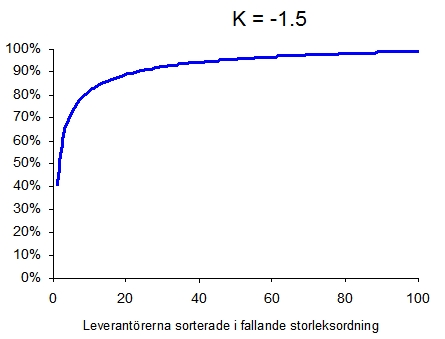
Medan en inköpsorganisation som arbetat hårt med att styra inköpet mot ramavtal och hovleverantörer kommer att få en struktur som kanske ser ut på följande sätt.
Exponentialfunktion k = -1.5
Finessen här är alltså att det bara är ett enda mätetal, k-värdet, som representerar strukturen. Det är förvisso lite merarbete att göra anpassningen, men den som är fingerfärdig i Excel fixar det på några minuter.
Grundarbetet, som beskrivits ovan, består i att koppla ihop spend, leverantörsnumerär och inköpskategorier. I förlängningen kan vi vilja koppla dessa data till parametrar såsom geografisk spridning eller leverantörernas faktiska storlek. Detta arbete kan göras på precis samma sätt; ABC eller exponentialfunktion.
Mer läsning:Klassifikation av leverantörer och inköpskategorier
